Ch. 16 Standardized and other formal assessments
Kevin Seifert and Rosemary Sutton

Understanding standardized testing is very important for beginning teachers as K-12 teaching is increasingly influenced by the administration and results of standardized tests. Teachers also need to be able to help parents and students understand test results. Consider the following scenarios.
- Vanessa, a newly licensed physical education teacher, is applying for a job at a middle school. During the job interview the principal asks how she would incorporate key sixth grade math skills into her PE and health classes as the sixth-grade students in the previous year did not attain Adequate Yearly Progress in mathematics.
- Danielle, a first-year science teacher in Ohio, is asked by Mr. Volderwell, a recent immigrant from Turkey and the parent of a tenth-grade son Marius, to help him understand test results. When Marius first arrived at school he took the Test of Cognitive Skills and scored on the eighty fifth percentile whereas on the state Science Graduation test he took later in the school year he was classified as “proficient” .
- James, a third-year elementary school teacher, attends a class in gifted education over summer as standardized tests from the previous year indicated that while overall his class did well in reading the top 20 per cent of his students did not learn as much as expected.
- Miguel, a 1st grade student, takes two tests in fall and the results indicate that his grade equivalent scores are 3.3 for reading and 3.0 for math. William’s parents want him immediately promoted into the second grade arguing that the test results indicate that he already can read and do math at the 3rd grade level. Greg, a first-grade teacher explains to William’s parents that a grade equivalent score of 3.3 does not mean William can do third grade work.

Understanding standardized testing is difficult as there are numerous terms and concepts to master and recent changes in accountability under the former No Child Left Behind Act of 2001 (NCLB) and current Elementary and Secondary Education Act of 2015 (ESEA), have increased the complexity of the concepts and issues. ESSA remains to be a test-based accountability system.
However, ESSA now allows schools to incorporate “one or more non-academic indicators that can help bring attention to the nation’s broader educational purposes.” (Mathis and Trujillo, 2016 p.3)
Link to: Every Student Succeeds Act (ESSA) – from the US Department of Education.
- In this chapter, we focus on the information that beginning teachers need to know and start with some basic concepts.
Basic concepts
Standardized tests are created by a team—usually test experts from a commercial testing company who consult classroom teachers and university faculty—and are administered in standardized ways. Students not only respond to the same questions, they also receive the same directions and have the same time limits. Explicit scoring criteria are used. Standardized tests are designed to be taken by many students within a state, province, or nation, and sometimes across nations. Teachers help administer some standardized tests and test manuals are provided that contain explicit details about the administration and scoring. For example, teachers may have to remove all the posters and charts from the classroom walls, read directions out loud to students using a script, and respond to student questions in a specific manner.
Criterion referenced standardized tests measure student performance against a specific standard or criterion.
- Criterion referenced tests currently used in US schools are often tied to state content standards and provide information about what students can and cannot do.
For example, one of the content standards for fourth grade reading in Kentucky is “Students will identify and describe the characteristics of fiction, nonfiction, poetry or plays” (Combined Curriculum Document Reading 4.1, 2006) and so a report on an individual student would indicate if the child can accomplish this skill. The report may state that number or percentage of items that were successfully completed (e.g. 15 out of 20, i.e. 75 per cent) or include descriptions such as basic, proficient, or advanced which are based on decisions made about the percent of mastery necessary to be classified into these categories.
Norm referenced standardized tests report students’ performance relative to others.
For example, if a student scores on the seventy-second percentile in reading it means she outperforms 72 percent of the students who were included in the test’s norm group. A norm group is a representative sample of students who completed the standardized test while it was being developed. For state tests, the norm group is drawn from the state, whereas for national tests the sample is drawn from the nation. Information about the norm groups is provided in a technical test manual that is not typically supplied to teachers, but should be available from the person in charge of testing in the school district.
- Reports from criterion and norm referenced tests provide different information.
Imagine a nationalized mathematics test designed to basic test skills in second grade. If this test is norm referenced, and Alisha receives a report indicating that she scored in the eighty-fifth percentile this indicates that she scored better than 85 per cent of the students in the norm group who took the test previously. If this test is criterion-referenced Alisha’s report may state that she mastered 65 percent of the problems designed for her grade level. The relative percentage reported from the norm-referenced test provides information about Alisha’s performance compared to other students, whereas the criterion referenced test attempts to describe what Alisha or any student can or cannot do with respect to whatever the test is designed to measure.
- When planning instruction, classroom teachers need to know what students can and cannot do so criterion referenced tests are typically more useful (Popham, 2004).
The current standard-based accountability and ESSA rely predominantly on criterion based tests to assess attainment of content-based standards. Consequently, the use of standardized norm referenced tests in schools has diminished and is largely limited to diagnosis and placement of children with specific cognitive disabilities or exceptional abilities (Haertel & Herman, 2005).
Some recent standardized tests can incorporate both criterion-referenced and norm referenced elements in the same test (Linn & Miller, 2005). That is, the test results not only provide information on mastery of a content standard, but also the percentage of students who attained that level of mastery.
Standardized tests can be high stakes i.e. performance on the test has important consequences. These consequences can be for students, e.g. passing a high school graduation test is required in order to obtain a diploma or passing PRAXIS II is a prerequisite to gain a teacher license.
Uses of standardized tests
- Standardized tests are used for a variety of reasons and the same test is sometimes used for multiple purposes.
Assessing students’ progress in a wider context
Well-designed teacher assessments provide crucial information about each student’s achievement in the classroom. However, teachers vary in the types of assessment they use so teacher assessments do not usually provide information on how students’ achievement compares to externally established criteria. Consider two eighth grade students, Brian and Joshua, who received As in their middle school math classes.
However, on the standardized norm referenced math test Brian scored in the fiftieth percentile whereas Joshua scored in the ninetieth percentile. This information is important to Brian and Joshua, their parents, and the school personnel. Likewise, two third grade students could both receive Cs on their report card in reading, but one may pass 25 per cent and the other 65 percent of the items on the Criterion Referenced State Test.
There are many reasons that students’ performance on teacher assessments and standardized assessments may differ. Students may perform lower on the standardized assessment because their teachers have easy grading criteria, or there is poor alignment between the content they were taught and that on the standardized test, or they are unfamiliar with the type of items on the standardized tests, or they have test anxiety, or they were sick on the day of the test.
Students may perform higher on the standardized test than on classroom assessments because their teachers have hard grading criteria, or the student does not work consistently in class (e.g. does not turn in homework) but will focus on a standardized test, or the student is adept at the multiple-choice items on the standardized tests, but not at the variety of constructing response and performance items the teacher uses. We should always be very cautious about drawing inferences from one kind of assessment.
In some states, standardized achievement tests are required for home-schooled students in order to provide parents and state officials information about the students’ achievement in a wider context. For example, in New York home-schooled students must take an approved standardized test every other year in grades four through eight and every year in grades nine through twelve. These tests must be administered in a standardized manner and the results filed with the Superintendent of the local school district. If a student does not take the tests or scores below the thirty-third percentile the home schooling program may be placed on probation (New York State Education Department, 2005).
Diagnosing student’s strengths and weaknesses
- Standardized tests, along with interviews, classroom observations, medical examinations, and school records are used to help diagnose students’ strengths and weaknesses.
Often the standardized tests used for this purpose are administered individually to determine if the child has a disability. For example, if a kindergarten child is having trouble with oral communication, a standardized language development test could be administered to determine if there are difficulties with understanding the meaning of words or sentence structures, noticing sound differences in similar words, or articulating words correctly (Peirangelo & Guiliani, 2002).
It would also be important to determine if the child was a recent immigrant, had a hearing impairment or intellectual impairment. The diagnosis of learning disabilities typically involves the administration of at least two types of standardized tests—an aptitude test to assess general cognitive functioning and an achievement test to assess knowledge of specific content areas as part of the special education process. (Peirangelo & Guiliani, 2006). We discuss the difference between aptitude and achievement tests later in this chapter.
Selecting students for specific programs
- Standardized tests are often used to select students for specific programs.
For example, the SAT (Scholastic Assessment Test) and ACT (American College Test) are norm referenced tests used to help determine if high school students are admitted to selective colleges. Norm referenced standardized tests are also used, among other criteria, to determine if students are eligible for special education or gifted and talented programs. Criterion referenced tests are used to determine which students are eligible for promotion to the next grade or graduation from high school.
Schools that place students in ability groups including high school college preparation, academic, or vocational programs may also use norm referenced or criterion referenced standardized tests. When standardized tests are used as an essential criterion for placement they are obviously high stakes for students.
Assisting teachers’ planning
- Norm referenced and criterion referenced standardized tests, among other sources of information about students, can help teachers make decisions about their instruction.
For example, if a social studies teacher learns that most of the students did very well on a norm referenced reading test administered early in the school year he may adapt his instruction and use additional primary sources. A reading teacher after reviewing the poor end-of the-year criterion referenced standardized reading test results may decide that next year she will modify the techniques she uses. A biology teacher may decide that she needs to spend more time on genetics as her students scored poorly on that section of the standardized criterion referenced science test.
These are examples of assessment for learning which involves data-based decision making. It can be difficult for beginning teachers to learn to use standardized test information appropriately, understanding that test scores are important information, but also remembering that there are multiple reasons for students’ performance on a test.
Accountability
- Standardized test results are increasingly used to hold teachers and administrators accountable for students’ learning.
Prior to 2002, many States required public dissemination of students’ progress, but under NCLB school districts in all states have been required to send report cards to parents and the public that include results of standardized tests for each school. Under ESSA, schools continue to be required to make student performance indicators publicly available, annually. (ASCD, 2015) Providing information about students’ standardized tests is not new as newspapers began printing summaries of students’ test results within school districts in the 1970s and 1980s (Popham, 2005).
However, public accountability of schools and teachers has been increasing in the US and many other countries and this increased accountability impacts the public perception and work of all teachers including those teaching in subjects or grade levels not being tested.
For example, Erin, a middle school social studies teacher, said:
“As a teacher in a ‘non-testing’ subject area, I spend substantial instructional time supporting the standardized testing requirements. For example, our school has instituted ‘word of the day’, which encourages teachers to use, define, and incorporate terminology often used in the tests (e.g. “compare”, “oxymoron” etc.). I use the terms in my class as often as possible and incorporate them into written assignments.
I also often use test questions of similar formats to the standardized tests in my own subject assessments (e.g. multiple-choice questions with double negatives, short answer and extended response questions) as I believe that practice in the test question formats will help students be more successful in those subjects that are being assessed.”
Accountability and standardized testing are two components of Standards Based Reform in Education that was initiated in the USA in 1980s.
Types of standardized tests
Achievement tests
Summarizing the past: K-12 achievement tests are designed to assess what students have learned in a specific content area. These tests include those specifically designed by states to access mastery of state academic content standards (see more details below) as well as general tests such as the California Achievement Tests, The Comprehensive Tests of Basic Skills, Iowa Tests of Basic Skills, Metropolitan Achievement Tests, and the Stanford Achievement Tests.
These general tests are designed to be used across the nation and so will not be as closely aligned with state content standards as specifically designed tests. Some states and Canadian Provinces use specifically designed tests to assess attainment of content standards and a general achievement test to provide normative information.
Standardized achievement tests are designed to be used for students in kindergarten through high school. For young children questions are presented orally, and students may respond by pointing to pictures, and the subtests are often not timed. For example, on the Iowa Test of Basic Skills designed for students are young as kindergarten the vocabulary test assesses listening vocabulary. The teacher reads a word and may also read a sentence containing the word. Students are then asked to choose one of three pictorial response options.
Achievement tests are used as one criterion for obtaining a license in a variety of professions including nursing, physical therapy, and social work, accounting, and law. Their use in teacher education is recent and is part of the increased accountability of public education and most States require that teacher education students take achievement tests to obtain a teaching license.
For those seeking middle school and high school licensure, these are tests are in the content area of the major or minor (e.g. mathematics, social studies); for those seeking licenses in early childhood and elementary the tests focus on knowledge needed to teach students of specific grade levels. The most commonly used tests, the PRAXIS series, tests I and II, developed by Educational Testing Service, include three types of tests (www.ets.org):
- Subject Assessments, these tests on general and subject-specific teaching skills and knowledge. They include both multiple-choice and constructed-response test items.
- Principles of Learning and Teaching (PLT) Tests assess general pedagogical knowledge at four grade levels: Early Childhood, K-6, 5-9, and 7-12. These tests are based on case studies and include constructed-response and multiple-choice items. Much of the content in this textbook is relevant to the PLT tests.
- Teaching Foundations Tests assess pedagogy in five areas: multi-subject (elementary), English, Language Arts, Mathematics, Science, and Social Science.
These tests include constructed-response and multiple-choice items which test teacher education students. The scores needed to pass each test vary and are determined by each state.
Diagnostic tests
Profiling skills and abilities: Some standardized tests are designed to diagnose strengths and weaknesses in skills, typically reading or mathematics skills. For example, an elementary school child may have difficulty in reading and one or more diagnostic tests would provide detailed information about three components: (1) word recognition, which includes phonological awareness (pronunciation), decoding, and spelling; (2) comprehension which includes vocabulary as well as reading and listening comprehension, and (3) fluency (Joshi 2003).
Diagnostic tests are often administered individually by school psychologists, following standardized procedures. The examiner typically records not only the results on each question, but also observations of the child’s behavior such as distractibility or frustration. The results from the diagnostic standardized tests are used in conjunction with classroom observations, school and medical records, as well as interviews with teachers, parents and students to produce a profile of the student’s skills and abilities, and where appropriate diagnose a learning disability.
Aptitude tests
Predicting the future: Aptitude tests, like achievement tests, measure what students have learned, but rather than focusing on specific subject matter learned in school (e.g. math, science, English or social studies), the test items focus on verbal, quantitative, problem solving abilities that are learned in school or in the general culture (Linn & Miller, 2005).
These tests are typically shorter than achievement tests and can be useful in predicting general school achievement. If the purpose of using a test is to predict success in a specific subject (e.g. language arts) the best prediction is past achievement in language arts and so scores on a language arts achievement test would be useful.
However, when the predictions are more general (e.g. success in college) aptitude tests are often used. According to the test developers, both the ACT and SAT Reasoning tests, used to predict success in college, assess general educational development and reasoning, analysis and problem solving as well as questions on mathematics, reading and writing (http://www.collegeboard.com; http://www.act.org/).
The SAT Subject Tests that focus on mastery of specific subjects like English, history, mathematics, science, and language are used by some colleges as entrance criteria and are more appropriately classified as achievement tests than aptitude tests even though they are used to predict the future.
Tests designed to assess general learning ability have traditionally been called Intelligence Tests but are now often called learning ability tests, cognitive ability tests, scholastic aptitude tests, or school ability tests. The shift in terminology reflects the extensive controversy over the meaning of the term intelligence and that its traditional use was associated with inherited capacity (Linn & Miller 2005).
The more current terms emphasize that tests measure developed ability in learning not innate capacity. The Cognitive Abilities Test assesses K-12 students’ abilities to reason with words, quantitative concepts, and nonverbal (spatial) pictures. The Woodcock Johnson IV contains cognitive abilities tests as well as achievement tests for ages 2 to 90 years.
High-stakes testing by states
While many States had standardized testing programs prior to 2000, the number of statewide tests has grown enormously since then because of the former NCLB, and current ESSA, require that all states test students in reading, mathematics annually in grades third through eighth and at least once in high school. Science assessments are given at least once in each grade span from grades 3-5, 6-9, and 10-12. (CCSSO, 2016).
Students with disabilities and English language learners must be included in the testing and be provided with appropriate accommodations. States are allowed to administer alternative assessments to no more than 1% of students with the most significant cognitive disabilities. (ASCD, 2015). In this section, we focus on these tests and their implications for teachers and students.
Standards based assessment Academic content standards
ESSA mandates that states must develop academic content standards that specify what students are expected to know or be able to do at each grade level.
An example, a broad standard in reading is:
“Students should be able to construct meaning through experiences with literature, cultural events and philosophical discussion” (no grade level indicated). (American Federation of Teachers, 2006, p. 6).
Standards that are too narrow can result in a restricted curriculum. An example of a narrow standard might be:
Students can define, compare and contrast, and provide a variety of examples of synonyms and antonyms.
A stronger standard is:
“Students should apply knowledge of word origins, derivations, synonyms, antonyms, and idioms to determine the meaning of words (grade 4) (American Federation of Teachers, 2006, p. 6).
The American Federation of Teachers conducted a study in 2005-6 and reported that some of the standards in reading, math and science were weak in 32 states. States set the strongest standards in science followed by mathematics. Standards in reading were particularly problematic and with one-fifth of all reading standards redundant across the grade levels, i.e. word-by-word repetition across grade levels at least 50 per cent of the time (American Federation of Teachers, 2006).
Even if the standards are strong, there are often so many of them that it is hard for teachers to address them all in a school year. Content standards are developed by curriculum specialists who believe in the importance of their subject area so they tend to develop large numbers of standards for each subject area and grade level.
At first glance, it may appear that there are only several broad standards, but under each standard there are subcategories called goals, benchmarks, indicators or objectives (Popham, 2004). For example, Idaho’s first grade mathematics standard, judged to be of high quality (AFT 2000) contains five broad standards, including 10 goals and a total of 29 objectives (Idaho Department of Education, 2005-6).
Alignment of standards, testing and classroom curriculum
The state tests must be aligned with strong content standards in order to provide useful feedback about student learning. If there is a mismatch between the academic content standards and the content that is assessed, then the test results cannot provide information about students’ proficiency on the academic standards.
Sampling content
When numerous standards have been developed it is impossible for tests to assess all of the standards every year, so the tests sample the content, i.e. Measure some, but not all the standards every year. Content standards cannot be reliably assessed with only one or two items so the decision to assess one content standard often requires not assessing another. This means if there are too many content standards a significant proportion of them are not measured each year.
In this situation, teachers try to guess which content standards will be assessed that year and align their teaching on those specific standards. Of course, if these guesses are incorrect students will have studied content, not on the test and not studied content that is on the test. Some argue that this is a very serious problem with current state testing and Popham (2004) an expert on testing even said: “What a muddleheaded way to run a testing program.” (p. 79)
A national survey of over 4,000 teachers indicated that the majority of teachers reported that the state mandated tests were compatible with their daily instruction and were based on curriculum frameworks that all teachers should follow. The majority of teachers also reported teaching test taking skills and encouraging students to work hard and prepare. Elementary school teachers reported a greater impact of the high stakes tests: 56 per cent reported the tests influenced their teaching daily or a few times a week compared to 46 percent of middle school teachers and 28 per cent of high school teachers.
Even though the teachers had adapted their instruction because of the standardized tests they were skeptical about them with 40 per cent reporting that teachers had found ways to raise test scores without improving student learning and over 70 per cent reporting that the test scores were not an accurate measure of what minority students know and can do (Pedulla, Abrams, Madaus, Russell, Ramos, & Miao; 2003).

International testing
Testing in the Canadian provinces
Canada has developed a system of testing in the provinces as well as national testing. Each province undertakes its own curriculum based assessments. At the elementary school level provinces assess reading and writing (language arts) as well as mathematics (also called numeracy).
In the middle grades science and social studies is often assessed in addition to language arts and mathematics. Summary results of these tests are published but there are no specific consequences for poor performance for schools. In addition, these tests are not high stakes for students. At the secondary school level, high stakes curriculum based exit tests are common.
Canada has developed pan-Canada assessment in mathematics, reading and writing, and science that are administered to a random sample of schools across the country. These assessments are intended to determine whether, on average, students across Canada reach similar levels of performance at about the same age. They are not intended to provide individual feedback to students are similar in purpose to the NAEP tests administered in the United States.
International comparisons
Along with the increasing globalization has come an interest with international comparisons in educational achievement and practices. In 2015 approximately 540,000 15-year old’s in schools from participating countries took the Program for International Assessment (PISA). (OECD, 2016)
PISA has assessed 15-year-olds in reading, mathematical and science literacy triennially since 2000. The items on both series of tests include multiple choice, short answer and constructed response formats and are translated into more than 30 languages.
Key Findings from PISA in Science
The United States remains in the middle of the rankings
Among the 35 countries in the OECD, the United States performed around average in science, the major domain of this assessment cycle. Its performance was also around average in reading, but below average in mathematics. There has been no significant change in science and reading performance since the last time they were the major domains (science in 2006 and reading in 2009).
One in five (20%) of 15-year-old students in the United States are low performers, not reaching the PISA baseline Level 2 of science proficiency. This proportion is similar to the OECD average of 21%, but more than twice as high as the proportion of low performers in Estonia, Hong Kong (China), Japan, Macao (China), Singapore and Viet Nam.
At the other end of the performance scale, 9% of students in the United States are top performers, achieving Level 5 or 6, comparable to the average of 8% across the OECD. By contrast, over 15% of 15-year-old students in Japan, Singapore and Chinese Taipei achieve this level of performance.
Students in the United States display high levels of epistemic beliefs, or those beliefs that correspond with currently accepted representations of the goal of scientific inquiry and the nature of scientific claims. Over nine in ten 15-yearolds in the United States agree that ideas in science sometimes change, that good answers are based on evidence from many different experiments and that it is good to try experiments more than once to be sure of one’s findings. (OECD, 2016)
Understanding test results
In order to understand test results from standardized tests it is important to be familiar with a variety of terms and concepts that are fundamental to “measurement theory”, the academic study of measurement and assessment. Two major areas in measurement theory, reliability and validity, were discussed in the previous chapter; in this chapter, we focus on concepts and terms associated with test scores.
The Basics
Frequency distributions
A frequency distribution is a listing of the number of students who obtained each score on a test. If 31 students take a test, and the scores range from 11 to 30 then the frequency distribution might look like Table 44. Plotting a frequency distribution helps us see what scores are typical and how much variability there are in the scores. We describe more precise ways of determining typical scores and variability next.
Table 44: Frequency distribution for 30 scores
| Score on test | Frequency | Central tendency measures |
| 17 | 1 | |
| 18 | 1 | |
| 19 | 0 | |
| 20 | 3 | |
| 21 | 2 | |
| 22 | 6 | Mode |
| 23 | 3 | Median |
| 24 | 2 | Mean |
| 25 | 0 | |
| 26 | 2 | |
| 27 | 6 | Mode |
| 28 | 2 | |
| 29 | 2 | |
| 30 | 1 | |
| TOTAL | 31 |
Central tendency and variability
There are three common ways of measuring central tendency or which score(s) are typical. The mean is calculated by adding up all the scores and dividing by the number of scores. The median is the “middle” score of the distribution—that is half of the scores are above the median and half are below. The median of the distribution is 23 because 15 scores are above 23 and 15 are below.
The mode is the score that occurs most often. In Table 44 there are two modes 22 and 27 and so this distribution is described as bimodal. Calculating the mean, median and mode are important as each provides different information for teachers.
The median represents the score of the “middle” students, with half scoring above and below, but does not tell us about the scores on the test that occurred most often.
The mean is important for some statistical calculations, but is highly influenced by a few extreme scores (called outliers) but the median is not. To illustrate this, imagine a test out of 20 points taken by 10 students, and most do very well but one student does very poorly. The scores might be 4, 18, 18, 19, 19, 19, 19, 19, 20, 20. The mean is 17.5 (170/10) but if the lowest score (4) is eliminated the mean is now is 1.5 points higher at 19 (171/9).
However, in this example, the median remains at 19 whether the lowest score is included. When there are some extreme scores the median is often more useful for teachers in indicating the central tendency of the frequency distribution.
The measures of central tendency help us summarize scores that are representative, but they do not tell us anything about how variable or how spread out are the scores. A simple way to summarize variability is the range, which is the lowest score subtracted from the lowest score.
However, the range is only based on two scores in the distribution, the highest and lowest scores, and so does not represent variability in all the scores. The standard deviation is based on how much, on average, all the scores deviate from the mean. In the exercise below we demonstrate how to calculate the standard deviation.
Calculating a standard deviation
Example: The scores from 11 students on a quiz are: 4, 7, 6, 3, 10, 7, 3, 7, 5, 5, and 9
- Order scores.
- Calculate the mean score.
- Calculate the deviations from the mean.
- Square the deviations from the mean.
- Calculate the mean of the squared deviations from the mean (i.e. sum the squared deviations from the mean then divide by the number of scores). This number is called the variance.
- Take the square root and you have calculated the standard deviation.
| Score(Step 1, order) | Deviation from the mean | Squared deviation from the mean | |
| 3 | -3 | 9 | |
| 3 | -3 | 9 | |
| 4 | -2 | 4 | (Step 4-5, complete the calculations) |
| 5 | -1 | 1 | Formula: |
| 5 | -1 | 1 | Standard deviation NN = Number of scores |
| 6 | 0 | 0 | |
| 7 | 1 | 1 | |
| 7 | 1 | 1 | |
| 7 | 1 | 1 | |
| 9 | 3 | 9 | |
| 10 | 4 | 4 | |
| TOTAL = 66 | 40 | ||
| (Step 2, calculate mean)MEAN66/11=6 | (Step 3, calculate deviations)Mean=40/11=3.64 | (Step 6, find the standard deviation)Standard deviation=3.64=1.91 |
Exhibit 21: Calculating a standard deviation
The normal distribution
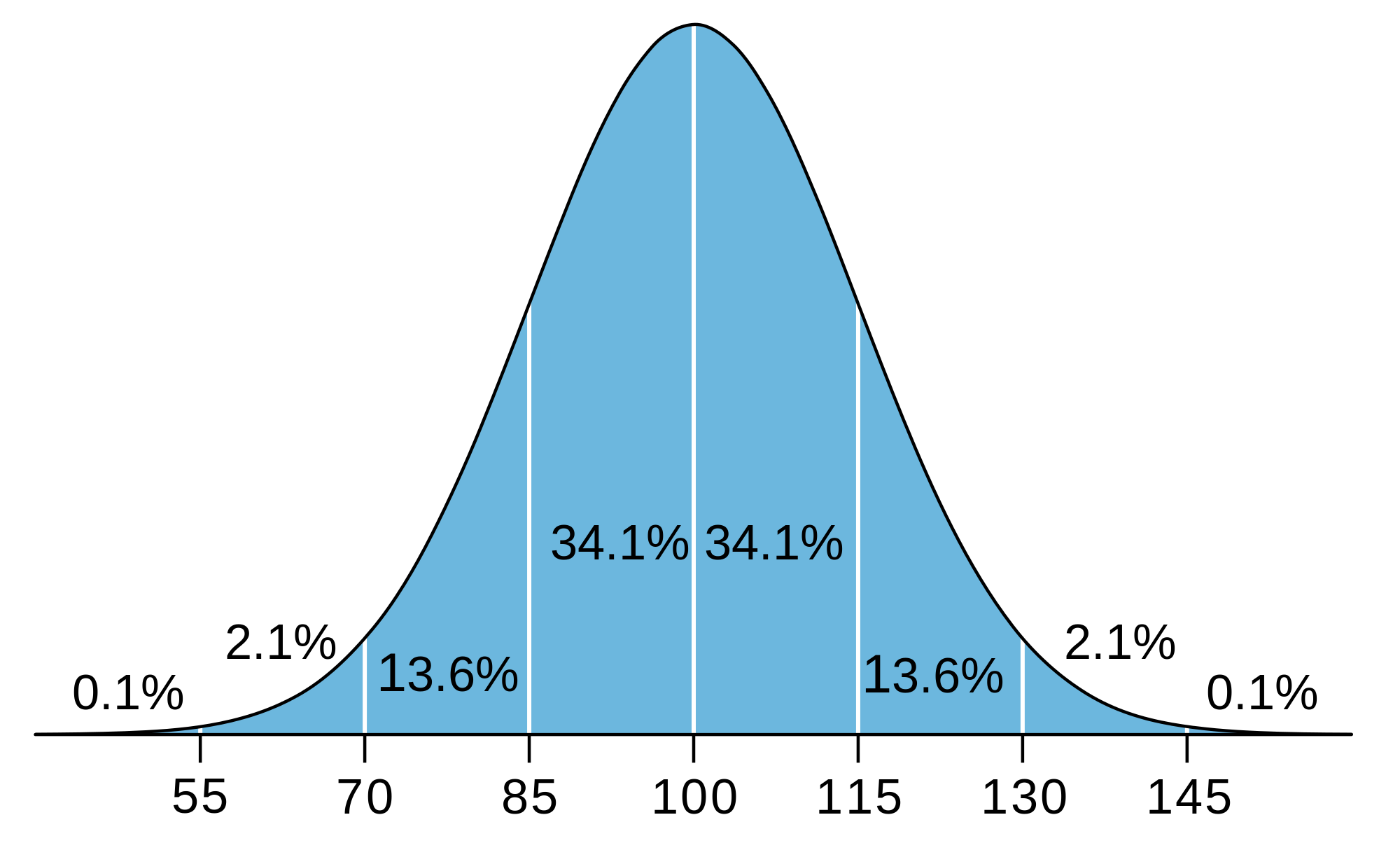
Knowing the standard deviation is particularly important when the distribution of the scores falls on a normal distribution. When a standardized test is administered to a very large number of students the distribution of scores is typically similar, with many students scoring close to the mean, and fewer scoring much higher or lower than the mean. When the distribution of scores looks like the bell shape is called a normal distribution. A normal distribution is symmetric, and the mean, median and mode are all the same.
Normal curve distributions are very important in education and psychology because of the relationship between the mean, standard deviation, and percentiles. In all normal distributions 34 percent of the scores fall between the mean and one standard deviation of the mean. Intelligence tests often constructed to have a mean of 100 and standard deviation of 15.
Wikimedia.org
In this example, 34 percent of the scores are between 100 and 115 and as well, 34 per cent of the scores lie between 85 and 100. This means that 68 percent of the scores are between -1 and +1 standard deviations of the mean (i.e. 85 and 115). Note than only 14 percent of the scores are between +1 and +2 standard deviations of the mean and only 2 percent fall above +2 standard deviations of the mean.
In a normal distribution, a student who scores the mean value is always in the fiftieth percentile because the mean and median are the same. A score of +1 standard deviation above the mean (e.g. 115 in the example above) is the 84 per cent tile (50 per cent and 34 per cent of the scores were below 115). In Exhibit 10 we represent the percentile equivalents to the normal curve and we also show standard scores.
Kinds of test scores
A standard score expresses performance on a test in terms of standard deviation units above of below the mean (Linn & Miller, 2005). There are a variety of standard scores:
Z-score: One type of standard score is a z-score, in which the mean is 0 and the standard deviation is 1. This means that a z-score tells us directly how many standard deviations the score is above or below the mean. For example, if a student receives a z score of 2 her score is two standard deviations above the mean or the eighty fourth percentile. A student receiving a z score of -1.5 scored one and one-half deviations below the mean. Any score from a normal distribution can be converted to a z score if the mean and standard deviation is known. The formula is:
Z−score=Score−mean score
Standard deviation
So, if the score is 130 and the mean is 100 and the standard deviation is 15 then the calculation is:
Z==2
T-score: A T-score has a mean of 50 and a standard deviation of 10. This means that a T-score of 70 is two standard deviations above the mean and so is equivalent to a z-score of 2.
Stanines: Stanines (pronounced stanines) are often used for reporting students’ scores and are based on a standard nine-point scale and with a mean of 5 and a standard deviation of 2. They are only reported as whole numbers and Figure 11-10 shows their relation to the normal curve.
Grade equivalent sores
A grade equivalent score provides an estimate of test performance based on grade level and months of the school year (Popham, 2005, p. 288). A grade equivalent score of 3.7 means the performance is at that expected of a third-grade student in the seventh month of the school year. Grade equivalents provide a continuing range of grade levels and so can be considered developmental scores. Grade equivalent scores are popular and seem easy to understand, however they are typically misunderstood.
If James, a fourth-grade student, takes a reading test and the grade equivalent score is 6.0; this does not mean that James can do sixth grade work. It means that James performed on the fourth-grade test as a sixth-grade student is expected to perform. Testing companies calculate grade equivalents by giving one test to several grade levels. For example, a test designed for fourth graders would also be given to third and fifth graders. The raw scores are plotted and a trend line is established and this is used to establish the grade equivalents.
Grade equivalent scores also assume that the subject matter that is being tested is emphasized at each grade level to the same amount and that mastery of the content accumulates at a mostly constant rate (Popham, 2005). Many testing experts warn that grade equivalent scores should be interpreted with considerable skepticism and that parents often have serious misconceptions about grade equivalent scores. Parents of high achieving students may have an inflated sense of what their child’s level of achievement is.
- In 1986 the International Reading Association stated that grade equivalents should NOT be used.
Because of the inherent psychometric problems associated with age and grade equivalents that seriously limit their reliability and validity, these scores should not be used for making diagnostic or placement decisions (Bracken, 1988; Reynolds, 1981).
Issues with standardized tests
Many people have very strong views about the role of standardized tests in education. Some believe they provide an unbiased way to determine an individual’s cognitive skills as well as the quality of a school or district. Others believe that scores from standardized tests are capricious, do not represent what students know, and are misleading when used for accountability purposes.
Many educational psychologists and testing experts have nuanced views and make distinctions between the information standardized tests can provide about students’ performances and how the test results are interpreted and used. In this nuanced view, many of the problems associated with standardized tests arise from their high stakes use such as using the performance on one test to determine selection into a program, graduation, or licensure, or judging a school as high vs low performing.
Are standardized tests biased?
- In a multicultural society, one crucial question is: Are standardized tests biased against certain social class, racial, or ethnic groups?
This question is much more complicated than it seems because bias has a variety of meanings. An everyday meaning of bias often involves the fairness of using standardized test results to predict potential performance of disadvantaged students who have previously had few educational resources.
For example, should Dwayne, a high school student who worked hard but had limited educational opportunities because of the poor schools in his neighborhood and few educational resources in his home, be denied graduation from high school because of his score on one test. It was not his fault that he did not have the educational resources and if given a chance with a change his environment (e.g. by going to college) his performance may blossom.
In this view, test scores reflect societal inequalities and can punish students who are less privileged, and are often erroneously interpreted as a reflection of a fixed inherited capacity. Researchers typically consider bias in more technical ways and three issues will be discussed: item content and format; accuracy of predictions, and stereotype threat.
Item content and format. Test items may be harder for some groups than others. An example of social class bias in a multiple-choice item asked students the meaning of the term field. The students were asked to read the initial sentence in italics and then select the response that had the same meaning of field (Popham 2004, p. 24):
My dad’s field is computer graphics.
- The pitcher could field his position
- We prepared the field by plowing it
- The doctor examined my field of vision
- What field will you enter after college?
Children of professionals are more likely to understand this meaning of field as doctors, journalists and lawyers have “fields”, whereas cashiers and maintenance workers have jobs so their children are less likely to know this meaning of field. (The correct answer is D).
Testing companies try to minimize these kinds of content problems by having test developers from a variety of backgrounds review items and by examining statistically if certain groups find some items easier or harder. However, problems do exist and a recent analysis of the verbal SAT tests indicated that whites tend to score better on easy items, whereas African Americans, Hispanic Americans and Asian Americans score better on hard items (Freedle, 2002). While these differences are not large, they can influence test scores.
Researchers think that the easy items involving words that are used in everyday conversation may have subtly different meanings in different subcultures whereas the hard words (e.g. vehemence, sycophant) are not used in every conversation and so do not have these variations in meaning. Test formats can also influence test performance. Females typically score better at essay questions and when the SAT recently added an essay component, the females overall SAT verbal scores improved relative to males (Hoover, 2006).
Accuracy of predictions
Standardized tests are used, among other criteria to determine who will be admitted to selective colleges. This practice is justified by predictive validity evidence—i.e. that scores on the ACT or SAT are used to predict first year college grades. Recent studies have demonstrated that the predictions for black and Latino students are less accurate than for white students and that predictors for female students are less accurate than male students (Young, 2004).
However, perhaps surprisingly the test scores tend to slightly over predict success in college for black and Latino students, i.e. these students are likely to attain lower freshman grade point averages than predicted by their test scores. In contrast, test scores tend to slightly under predict success in college for female students, i.e. these students are likely to attain higher freshman grade point averages than predicted by their test scores. Researchers are not sure why there are differences in how accurately the SAT and ACT test predict freshman grades.
Stereotype threat
Groups that are negatively stereotyped in some area, such as women’s performance in mathematics, are in danger of stereotype threat, i.e. concerns that others will view them through the negative or stereotyped lens (Aronson & Steele, 2005). Studies have shown that test performance of stereotyped groups (e.g. African Americans, Latinos, women) declines when it is emphasized to those taking the test that (a) the test is high stakes, measures intelligence or math and (b) they are reminded of their ethnicity, race or gender (e.g. by asking them before the test to complete a brief demographic questionnaire).
Even if individuals believe they are competent, stereotype threat can reduce working memory capacity because individuals are trying to suppress the negative stereotypes. Stereotype threat seems particularly strong for those individuals who desire to perform well.
- Standardized test scores of individuals from stereotyped groups may significantly underestimate their actual competence in low stakes testing situations.
Do teachers teach to the tests?
There is evidence that schools and teachers adjust the curriculum so it reflects what is on the tests and also prepares students for the format and types of items on the test. Several surveys of elementary school teachers indicated that more time was spent on mathematics and reading and less on social studies and sciences in 2004 than 1990 (Jerald, 2006). Principals in high minority enrollment schools in four states reported in 2003 they had reduced time spent on the arts.
Recent research in cognitive science suggests that reading comprehension in a subject (e.g. science or social studies) requires that students understand a lot of vocabulary and background knowledge in that subject (Recht & Leslie, 1988). This means that even if students gain good reading skills they will find learning science and social studies difficult if little time has been spent on these subjects.
Taking a test with an unfamiliar format can be difficult, so teachers help students prepare for specific test items and formats (e.g. double negatives in multiple choice items; constructed response).
- There is growing concern that the amount of test preparation that is now occurring in schools is excessive and students are not being educated, but trained to do tests (Popham, 2004).
Chapter summary
Standardized tests are developed by a team of experts and are administered in standard ways. They are used for a variety of educational purposes including accountability. Most elementary and middle school teachers are likely to be responsible for helping their students attain state content standards and achieve proficiency on criterion referenced achievement tests.
In order for teachers to interpret test scores and communicate that information to students and parents they have to understand basic information about measures of central tendency and variability, the normal distribution, and several kinds of test scores. Current evidence suggests that standardized tests can be biased against certain groups and that many teachers tailor their curriculum and classroom tests to match the standardized tests.
Key terms
- Achievement tests
- Aptitude tests
- Criterion referenced tests
- Diagnostic tests
- Frequency distribution
- Grade equivalent scores
- High stakes tests
- Mean
- Median
- Mode
- Norm referenced tests
- Range
- Standard deviation
- Stanine
- Z-score
On the Internet
The National Center for Research on Evaluation, Standards, and Student Testing (CRESST) at UCLA focuses on research and development that improves assessment and accountability systems. It has resources for researchers, K-12 teachers, and policy makers on the implications of NCLB as well as classroom assessment.
This is the home page of Educational Testing Services (ETS) which administers the PRAXIS II series of tests and has links to the testing requirements for teachers seeking licensure in each state District of Columbia and the US Virgin Islands.
References
Seifert, K. and Sutton, R. (2009). Educational Psychology. Saylor Foundation. (Chapter 12) Retrieved from https://open.umn.edu/opentextbooks/BookDetail.aspx?bookId=153

