31 5.1 Angular Position and Displacement
We’ve previously studied motion along a straight line and introduced such concepts as displacement, velocity, and acceleration.Then we dealt with motion of one point in two dimensions. Projectile motion is a special case of two-dimensional kinematics in which the object is projected into the air, while being subject to the gravitational force (constant acceleration). It’s trajectory is predictable using equations of uniformly accelerated motion. In this chapter, we consider situations where the objects rotate about a point (the axis of rotation) while traveling in a circular path. We typically consider the movement of an entire segment.
Rigid Bodies
An assumption made in biomechanics is that body segments are rigid bodies. Rigid bodies maintains a constant length. Instead of representing motion relative to a point (ex: center of mass) as we did in linear kinematics, we will represent motion of a rigid body (ex: thigh). This will affect our frame of reference as movement no longer occur in the x and y-axis. That’s right, we no longer describe movement in relation to the x and the y axis of a coordinate system but in relation to the axis of rotation.
Angle
An angle is formed at the intersection of two lines, two planes or a line and a plane. Angles are used to define the orientation of these lines or planes relative to each other.
Frame of Reference
Angular motion occurs about an axis of rotation. In the human body, this axis of rotation is a joint and the rigid bodies are the bones rotating about the angle. The axis is always perpendicular to the plane. For example. if we are interested in knee angle in the sagittal plane, we’ll be quantifying motion about the mediolateral axis. The frame of reference is no longer a cartesian reference system with two orthogonal axis but a combination of the axis of rotation and a reference axis. In this course, rotation about the axis of rotation in the clockwise direction will always be negative and rotation in the counterclockwise direction will always be positive.
Do you remember the difference between absolute and relative angles? In absolute angles, the angle of a body segment is reported relative to the horizontal plane. The horizontal plane represents a fixed reference. With relative angles, we measure the angle between two body segments or lines. In this case, both lines are capable of moving.
Angular Position (θ)
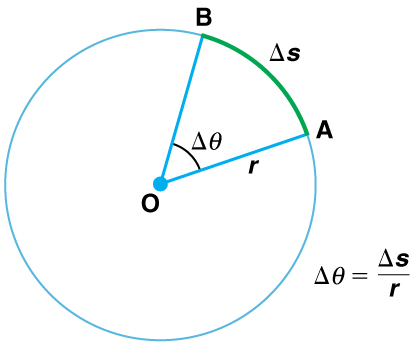
This result is the basis for defining the units used to measure rotation angles, Δθ to be radians(rad), defined so that
A comparison of some useful angles expressed in both degrees and radians is shown in Table 1.
| [latex]\textbf{Degree Measures}[/latex] | [latex]\textbf{Radian Measure}[/latex] |
|---|---|
| [latex]\boldsymbol{30^0}[/latex] | [latex]\boldsymbol{\frac{\pi}{6}}[/latex] |
| [latex]\boldsymbol{60^0}[/latex] | [latex]\boldsymbol{\frac{\pi}{3}}[/latex] |
| [latex]\boldsymbol{90^0}[/latex] | [latex]\boldsymbol{\frac{\pi}{2}}[/latex] |
| [latex]\boldsymbol{120^0}[/latex] | [latex]\boldsymbol{\frac{2\pi}{3}}[/latex] |
| [latex]\boldsymbol{135^0}[/latex] | [latex]\boldsymbol{\frac{3\pi}{4}}[/latex] |
| [latex]\boldsymbol{180^0}[/latex] | [latex]\boldsymbol{\pi}[/latex] |
| Table 1. Comparison of Angular Units. | |
range of motion = θ2– θ1
Another use of angular displacement in sport is counting the number of full body rotations. The number of twists or somersault performed in sports like diving, gymnastics or snowboarding for example, determine the level of difficulty of the performance. This aspect is important for the judges who attribute a score to the performance.
The angular displacement of a swing (range of motion) in sports like golf, tennis or hockey, affects the manner in which the ball is hit in these sports. See the relationship between angular displacement of a segment (ex: hockey stick) and the resulting linear displacement of a point (ex: the hockey puck) below:
Angular and Linear Displacement
In angular kinematics we describe the movement of a segment or rigid body as it rotates about a point. This segment could be described as a series of points who must each move linearly to accomplish this change in position. The linear displacement of each point is unique to the point and depends on how far it is located from the axis of rotation. The distance from the axis of rotation to the point of interest is called the radius (r).
Let’s consider two points ( a and b) along a segment. Let’s say we are interested in the movement of the arm during a jumping jack. We observe the movement in the frontal plane and measure a change in position from 0 degrees to 180 degrees as the participant moves their arm up over their head. Point a is located on the elbow and point b is located on the wrist. Both point a and point b must move through 180 degrees. In fact, every point on the arm must move through 180 degrees. But each point on the arm moves a different linear distance to accomplish this angular displacement of 180 degrees. Points closest to the shoulder joint (the point of rotation) don’t have to linearly travel as far as points closest to the hands to cover the 180 degrees. Point a (elbow) has a smaller linear displacement than point b (wrist). Point a has a shorter radius than point b, thus the linear displacement correlates to how far the point is from the axis of rotation (r).
This relationship is expressed with the following equation:
d = rθ
Note that angular position/displacement MUST be expressed in rads (not degrees or revolutions) for this relationship to be accurate.
Section Summary
- Uniform circular motion is motion in a circle at constant speed. The rotation angle Δθ is defined as the ratio of the arc length to the radius of curvature:
[latex]\boldsymbol{\Delta\theta\:=}\boldsymbol{\frac{\Delta{s}}{r}},[/latex]
where arc length Δs is distance traveled along a circular path and r is the radius of curvature of the circular path. The quantity Δθ is measured in units of radians (rad), for which
[latex]\boldsymbol{2\pi\textbf{ rad}=360^0=1\textbf{ revolution}}.[/latex] - The conversion between radians and degrees is 1 rad = 57.3°.
- Angular displacement defines the movement of a segment as represents the change in angular position.
- Linear displacement of any point along a segment that is rotation can be calculated with: d = rθ as long as angular position is expressed in rads.
Glossary
- arc length
- Δs, the distance traveled by an object along a circular path.
- rotation angle
- the ratio of the arc length to the radius of curvature on a circular path:
[latex]\boldsymbol{\Delta\theta\:=}\boldsymbol{\frac{\Delta{s}}{r}}[/latex]
- radius of curvature
- radius of a circular path
- radians
- a unit of angle measurement

