34 5.4 Linear Accelerations
When a limb is rotating at an increasing angular velocity, the tangential (linear) velocity of a point on the limb is increasing as well. The angular and linear accelerations of a point are related but unlike velocity, there are two linear accelerations to consider on rotation objects: tangential and centripetal acceleration.
Tangential Acceleration
The linear acceleration tangent to the circular path of a point on a rotating segment is called: tangential acceleration. It represents the chance in tangential (linear) velocity discussed in the previous section. Tangential acceleration is related to angular acceleration in the following way:
at = αr
Keep in mind that in order for this equation to be true, angular acceleration must be expressed in rads/s2.
Tangent: a line is tangent to a circle if the line intersects the circle at just one point. A line from this point to the centre of the circle (radius) is perpendicular to the tangent line.
Centripetal Acceleration
We know from kinematics that acceleration is a change in velocity, either in its magnitude or in its direction, or both. In uniform circular motion, the direction of the velocity changes constantly, so there is always an associated acceleration, even though the magnitude of the velocity might be constant. You experience this acceleration yourself when you turn a corner in your car. (If you hold the wheel steady during a turn and move at constant speed, you are in uniform circular motion.) What you notice is a sideways acceleration because you and the car are changing direction. The sharper the curve and the greater your speed, the more noticeable this acceleration will become. In this section we examine the direction and magnitude of that acceleration.
Figure 1 shows an object moving in a circular path at constant speed. The direction of the instantaneous velocity is shown at two points along the path. Acceleration is in the direction of the change in velocity, which points directly toward the center of rotation (the center of the circular path). This pointing is shown with the vector diagram in the figure. We call the acceleration of an object moving in uniform circular motion (resulting from a net external force) the centripetal acceleration (ac); centripetal means “toward the center” or “center seeking.”
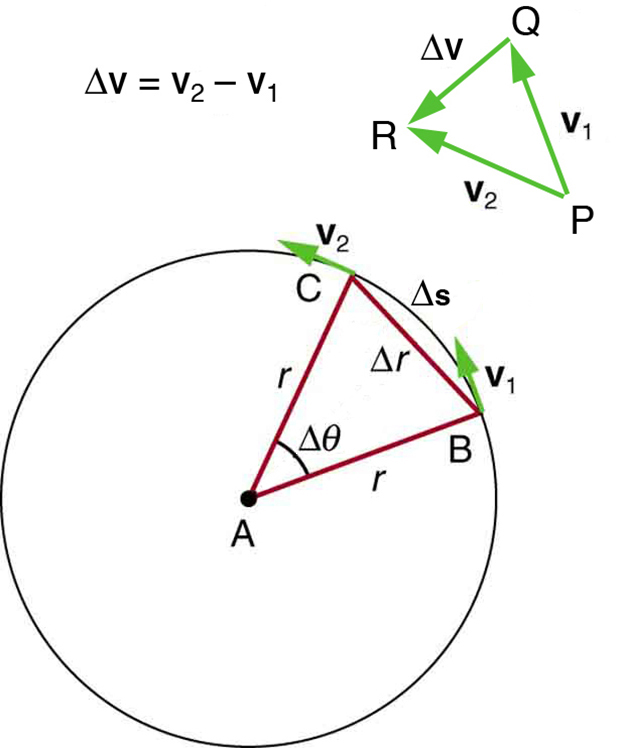
The direction of centripetal acceleration is toward the center of curvature, but what is its magnitude? Note that the triangle formed by the velocity vectors and the one formed by the radii r and Δs are similar. Both the triangles ABC and PQR are isosceles triangles (two equal sides). The two equal sides of the velocity vector triangle are the speeds v1 = v2 = v. Using the properties of two similar triangles, we obtain
Acceleration is Δv/Δt, and so we first solve this expression for Δv:
Then we divide this by Δt, yielding
Finally, noting that Δv/Δt = ac and that Δs/Δt = v, the linear or tangential speed, we see that the magnitude of the centripetal acceleration is
which is the acceleration of an object in a circle of radius r at a speed v. So, centripetal acceleration is greater at high speeds and in sharp curves (smaller radius), as you have noticed when driving a car. But it is a bit surprising that ac is proportional to speed squared, implying, for example, that it is four times as hard to take a curve at 100 km/h than at 50 km/h. A sharp corner has a small radius, so that ac is greater for tighter turns, as you have probably noticed.
It is also useful to express ac in terms of angular velocity. Substituting v = rω into the above expression, we find ac = (rω)2/r = rω2. We can express the magnitude of centripetal acceleration using either of two equations:
Recall that the direction of ac is toward the center. You may use whichever expression is more convenient, as illustrated in examples below.
Example 1: How Does the Centripetal Acceleration of a Car Around a Curve Compare with That Due to Gravity?
What is the magnitude of the centripetal acceleration of a car following a curve of radius 500 m at a speed of 25.0 m/s (about 90 km/h)? Compare the acceleration with that due to gravity for this fairly gentle curve taken at highway speed. See Figure 2(a).
Strategy
Because v and r are given, the first expression in [latex]\boldsymbol{a_{\textbf{c}}=\frac{v^2}{r};\:a_{\textbf{c}}=r\omega^2}[/latex] is the most convenient to use.
Solution
Entering the given values of v = 25.0 m/s and r = 500 m into the first expression for ac gives
Discussion
To compare this with the acceleration due to gravity (g = 9.80 m/s2), we take the ratio of ac /g = (1.25 m/s2)/(9.80m/s2) = 0.128. Thus, ac = 0.128 g and is noticeable especially if you were not wearing a seat belt.
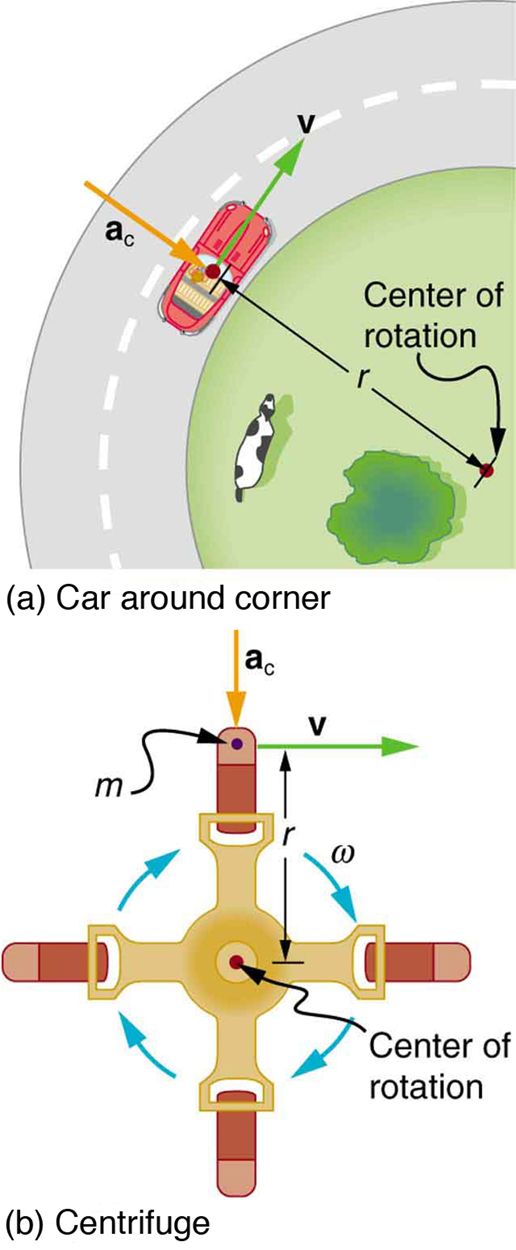
Of course, a net external force is needed to cause any acceleration, just as Newton proposed in his second law of motion. So a net external force is needed to cause a centripetal acceleration.
Section Summary
- Centripetal acceleration ac is the acceleration experienced while in uniform circular motion. It always points toward the center of rotation. It is perpendicular to the linear velocity[latex]\boldsymbol{v}[/latex]and has the magnitude
- The unit of centripetal acceleration is m/s2.
Conceptual Questions
1: Can centripetal acceleration change the speed of circular motion? Explain.
Problems & Exercises
1: A runner taking part in the 200 m dash must run around the end of a track that has a circular arc with a radius of curvature of 30 m. If he completes the 200 m dash in 23.2 s and runs at constant speed throughout the race, what is the magnitude of his centripetal acceleration as he runs the curved portion of the track?
2: Olympic ice skaters are able to spin at about 5 rev/s.
(a) What is their angular velocity in radians per second?
(b) What is the centripetal acceleration of the skater’s nose if it is 0.120 m from the axis of rotation?
(c) An exceptional skater named Dick Button was able to spin much faster in the 1950s than anyone since—at about 9 rev/s. What was the centripetal acceleration of the tip of his nose, assuming it is at 0.120 m radius?
(d) Comment on the magnitudes of the accelerations found. It is reputed that Button ruptured small blood vessels during his spins.
3: Unreasonable Results
A mother pushes her child on a swing so that his speed is 9.00 m/s at the lowest point of his path. The swing is suspended 2.00 m above the child’s center of mass.
(a) What is the magnitude of the centripetal acceleration of the child at the low point?
(b) What is the magnitude of the force the child exerts on the seat if his mass is 18.0 kg?
(c) What is unreasonable about these results?
(d) Which premises are unreasonable or inconsistent?
Glossary
- centripetal acceleration
- the acceleration of an object moving in a circle, directed toward the center
- ultracentrifuge
- a centrifuge optimized for spinning a rotor at very high speeds
Solutions
Problems & Exercises
2: (a) [latex]\boldsymbol{31.4\textbf{ rad/s}}[/latex] (b) [latex]\boldsymbol{118\textbf{ m/s}}[/latex] (c) [latex]\boldsymbol{384\textbf{ m/s}}[/latex] (d) The centripetal acceleration felt by Olympic skaters is 12 times larger than the acceleration due to gravity. That’s quite a lot of acceleration in itself. The centripetal acceleration felt by Button’s nose was 39.2 times larger than the acceleration due to gravity. It is no wonder that he ruptured small blood vessels in his spins.
3: (a) [latex]\boldsymbol{40.5\textbf{ m/s}^2}[/latex] (b) $\boldsymbol{905\textbf{ N}}$ (c) The force in part (b) is very large. The acceleration in part (a) is too much, about 4 g. (d) The speed of the swing is too large. At the given velocity at the bottom of the swing, there is enough kinetic energy to send the child all the way over the top, ignoring friction.

